|
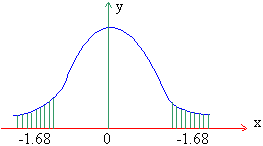
Example For z, find the probability
i) z ³ 1.68, ii) z £
1.68, iii) z £ -1.68, and iv) |
z | ³ 1.68.
Solution : i) P ( z ³
1.68 ) = 0.5 - P (0 £ 0 £
1.68)
= 0.5 - 4535 = 0.0465 »
5% of area.
ii) The probability that z £
1.68 is equal to the
area to the left of z = 1.68. Hence the required
area = 0.5 + 4.4535 = 0.9535.
iii) The probability that z £
-1.68 is equal to the
area to left of z = -1.68 = the area to the right of
( z = 1.68) = 0.5 - 0.4535 = 0.0465
iv) We know that | z | ³
1.68 Þ
z ³
1.68 or - z ³
1.68
i.e. z ³
1.68 or z £
1.68
i.e. z is to the right of 1.68 or z is to the left of
-1.68 <
P ( z ³
1.68 ) = 0.0465 and P ( z £
- 1.68 )
= 0.0465
Therefore P ( | z | ³
1.68 ) = 2 ´
0.0465 = 0.093
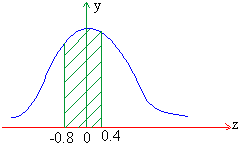
Example In a sample of 1000 cases,
the mean of a certain test is 14 and standard deviation is 2.5.
Assuming the distribution to be normal.
1) How many students score between 14 and 15 ?
2) How many score above 18 ?
3) How many score below 18 ?
4) How many score 16 ?
Solution : n = 1000, m
= 14 and s = 2.5
1) 
[next page]
|