|
The area lying between - 0.8 to 0.4
= Area ( z = 0 to z = 0.8) + Area ( z = 0 to z = 0.4)
= P ( 0 £
x £
0.8 ) + P ( 0 £
x £
0.4 )
= 0.2881 + 0.1554
= 0.4435
The required number of students score between 14 and 15
= NP = 1000 ´
0.4435 = 443.5 = 444.
2) z = 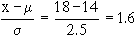
Area right to 1.6
= 0.5 - Area ( z = 0 to z = 1.6 )
= 0.5 - P ( 0 £
z £
1.6)
= 0.5 - 0.4452
= 0.0548
Therefore, the number of students score above 16 = nP
= 1000 ´
0.0548
= 54.8 = 55
3) z = 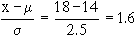
Area left to z = -2.4
= 0.5 - Area ( z = 0 to z = 2.4)
= 0.5 - 0.4918 = 0.0082
Therefore, the number of students score
below 8 = NP
= 1000 ´
0.0082
= 8.2
= 8
4) Exactly 16 means between x = 15.5 and x = 16.5

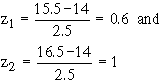
The area lying between z = 0.6 and z = 1
= Are ( z = 0 to z = 1 ) - Area (z = 0 to z = 0.6)
= 0.3413 - 0.225
= 0.1156
The number of students score exactly 16 = NP
= 1000 ´
0.1156
= 115.6
= 116
Example Ten thousand candidates appeared in a certain examination, having maximum marks as 100. It was found that the marks are normally distributed with mean as 39.5 and S. D. as 12.5. Determine approximately the number of candidates who secured a first class for which a minimum of 60 marks is necessary. You may see the given table below :
z = x/6 1.5 1.6 1.7 .8
A 0.93319 0.94520 0.95543 0.96407
Solution : m = 39.5 , s = 12.5 and x = 60
then z =
Now Area for z = 1.6 is 0.94520
Area for
z = 1.7 is 0.95543
Therefore difference for 0.1 is 0.01023
Therefore difference for 0.4 is 0.004092

Area for 1.64 = 0.94520 + 0.004092
= 0.949292
Area right to z = 1.64 = 1 - 0.949292 = 0.050708
Therefore the number of candidates who
secured 60 marks or more ( i.e. 1st class) = NP
= 1000 ´
0.50708
= 507.08
= 507
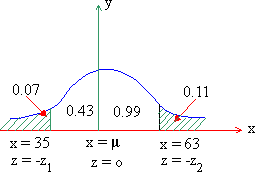
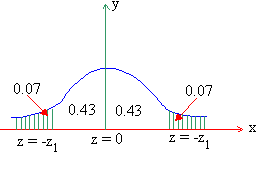
Example In a distribution exactly normal
7% of the items are under 35 and 89% are under 63. What are the
mean and standard deviations of the distribution ?
Solution : If x is normally distributed, N (m, s), then it is given that P ( x < 35 ) = 0.07 and P ( x < 63 ) = 0.89 or P ( x > 63 ) = 0.11
[next page]
|