|
Therefore  or m =
or m =  = E (X)
= E (X)
i.e. Mean = E(X) = Expected value.
Also variance (X) = s
x2 = 
On simplification, we get, the standard deviation,
i.e. s x2 = 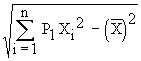
Example A business can make a profit
of $2000/- with the probability 0.4 or it can have a loss of $1000/-
with the probability 0.6. What is the expected profit ?
Solution : The discrete random variable
‘x’ is
x1 = $ 2000 (profit)
x2 = - $1000 (loss)
With probabilities P1 = 0.4 and P2 = 0.6 respectively
Then expected profit is given by,
E(x) = P1x1
+ P2x2
= (0.4) (2000) + (0.6) (-1000)
= $ 200
Example What is the expected value
of the number of points that will be obtained in a single throw
of an ordinary dice ?
Solution : The discrete random variable
‘x’, in this problem assume values
x1 = 1, x2 = 2, x3 = 3, x4 = 4, x5 = 5 and x6 = 6
With probabilities P1 = P2 = P3 = P4 = P5 = P6 = 1/6 (each)
Expected value of the number of points is given by,
E(x) = P1x1 + P2 x2
+ P3x3 + P4 x4 + P5
x5 + P6 x6 = 
[next page]
|