|
Example The odds in favor of A winning
a race against B are 5 : 2. If three races are attended, what are
the odds in favor of A winning at least one race ?
Solution : P (A winning) = 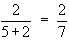
P (A losing) = 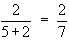
P (A winning the race at least once)
= 1 - P ( A losing all)
= 1 - P (A losing first) ´
P (A losing second) ´ P (A losing
third)
= 1 - 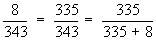
= 1 - 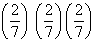
i.e. odds in favor of A winning at least one race are 335.8.
Example A book contains 1000 pages. A page
is chosen randomly. what is the chance the sum of the digits on a
page is equal to 9 ?
Solution : A page is selected randomly out of thousand
pages
\ n (s) = 1000C1 = 1000
Let A : A page selected which has a sum of digits on it be 9.
Number of favorable ways of getting a page, showing the no of the digits on
it 9 is .... {9, 18, 27, 36, 45, ........900}
\ n (A) = 100
Note that the sequence in the bracket is an A.P.
With a = 9, l = 900 and d = 9
Then l = a + (n - 1) d gives
\ 900 = 9 + (n - 1)
. 9
\ 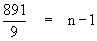
\ 99 = n
- 1
\ 100 = n
\ 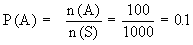
[next page]
|