Thus probability of passing at least two subjects
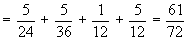
Therefore, probability of passing A and at least two subjects
Example Probability that a man will
be alive 25 years is 0.3 and that his wife will be alive 25 years
is 0.4. Find the probability that 25 years hence (1) Both will be
alive (2) Only man will be alive (3) Only wife will be alive (4)
At least one of them will be alive.
Solution :
Let A : the man will be alive 25 years hence \
P(A) = 0.3
Let B : His wife will be alive 25 years hence \ P(B)
= 0.4
(1) P (both will be alive)
= P (A) ´ P (B)
= 0.3
´ 0.4
= 12
(2) P (only man will be alive) =
P (A) ´ P (B)
= P (A) ´
[1 - P (B)]
= 0.3
´ [1 - 0.4]
= 0.3
´ 0.6
= 0.18
(3) P (only wife will be alive) = P
(B) ´ P (A)
= P(B) ´ [1 - P(A)]
= 0.4 ´
[1 - 0.3]
= 0.4 ´
0.7
= 0.28
(4) P (at least one of them
will be alive) = 1 - P(A) . P(B)
= 1 - (0.7) (0.6)
= 1 - 0.42
= 0.58
Example A box contains 6 white and
4 black balls. Two balls are drawn at random one after the other.
Replace the first ball after noting its color. Find the probability
that (1) both are white (2) both are black (3) the first is white,
the second is black (4) the first black the second white (5) one
white and one black.
Solution : Since the first ball is replaced,
the outcome of the second draw is no way affected i.e. the events
are independent.
[next page]
|