Event A : The score on the second die > the score on the 1st die.

i.e. A = { (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 3), (2, 4), (2, 5), (2, 6) (3, 4), (3, 5), (3, 6) (4, 5), (4, 6) (5, 6)}

\ n (A) = 15

Therefore, p (A) =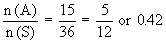

Example A coin is tossed three times. Find the probability of getting at least one head.

Solution : Experiment : A coin is tossed three times.

Sample space : S = {(H H H), (H H T), (HTH), (HTT), (THT), (TTH), (THH), (TTT) }

Þ n (S) = 8

Event A : getting at least one head

so that A : getting no head at all

= { (TTT) Þ n () = 1

P () =

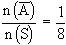
Therefore, P (A) = 1 - P ( A ) =

Example A ball is drawn at random from a box containing 6 red balls, 4 white balls and 5 blue balls. Determine the probability that the ball drawn is (i) red (ii) white (iii) blue (iv) not red (v) red or white.

Solution : Let R, W and B denote the events of drawing a red ball, a white ball and a blue ball respectively.

(i)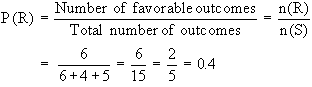    

[next page]

Index

7. 1 Introduction
7.2 Trial
7.3 Sample Space
7. 4 Definition of Probability
7. 5 The Laws of Probability
7. 6 Conditional Probability
7. 7 Theoretical Distribution
7. 8 Binomial Distribution
7. 9 Normal Distribution
Chapter 8