|
5.10 Kurtosis
It has its origin in the Greek word "Bulginess." In statistics it is the degree of flatness or ’peakedness’ in the region of mode of a frequency curve. It is measured relative to the ’peakedness’ of the normal curve. It tells us the extent to which a distribution is more peaked or flat-topped than the normal curve. If the curve is more peaked than a normal curve it is called ’Lepto Kurtic.’ In this case items are more clustered about the mode. If the curve is more flat-toped than the more normal curve, it is Platy-Kurtic. The normal curve itself is known as "Meso Kurtic."
Click here to enlarge
Moments
Moment is a familiar mechanical term for the measure of a force with reference to its tendency to produce rotation. In statistics moments are used to describe the various characteristics of a frequency distribution like center tendency, variation, skewness and kurtosis.
Moments are calculated using the arithmetic mean. According
to Waugh, the arithmetic mean of the various powers of these deviations
in any distribution are called the moments of the distribution.
Let ’ x ’ be the deviation of any item in a distribution from the
arithmetic mean of that distribution. The arithmetic mean of the
various powers of these deviations is the moments of the distribution.
if we take the mean of the 1st power of the deviations, we get the
1st moment about the mean, the mean of the squares of the deviations
gives the second moment about the mean, the mean of the cubes gives
the third moment about the mean and so on. The moments about mean
are called the "central moment" and are denoted by m1,
m2, m3, m4
....
Symbolically m1 =
 1st
central moment = 0
Since sum of deviations of items from the arithmetic mean is always zero.
m2 =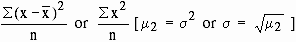 
m3 =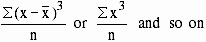
[next page]
|
Index
5.1 Introduction
5.2 Methods of computing dispersion
5.3 Range
5.4 Mean Deviation
5.5 Variance
5.6 Coefficient of Variation
5.7 Percentile
5.8 Quartiles and interquartile range
5.9 Skewness moments and Kurtosis
5.10 Kurtosis
Chapter 6
|
