|
5.4 Mean Deviation
Average deviations ( mean deviation ) is the average amount of variations (scatter) of the items in a distribution from either the mean or the median or the mode, ignoring the signs of these deviations by Clark and Senkade.
Individual Series
Steps : (1) Find the mean or median
or mode of the given series.
(2) Using and one of three, find the deviations ( differences ) of the items of the series from them.
i.e. xi - x, xi - Me and xi - Mo.
Me = Median and Mo = Mode.
(3) Find the absolute values of these deviations i.e. ignore there positive (+) and negative (-) signs.
i.e. | xi - x | , | xi - Me | and xi - Mo |.
(4) Find the sum of these absolute deviations.
i.e. S | xi - x | + , S | xi - Me | , and S | xi - Mo | .
(5) Find the mean deviation using the following formula.
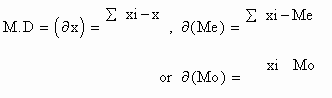
Note that :
(i) generally M. D. obtained from the median is the best for the practical purpose.
(ii) co-efficient of M. D. =
Example Calculate Mean deviation and its
co-efficient for the following salaries:
$ 1030, $ 500, $ 680, $ 1100, $ 1080, $ 1740. $ 1050, $ 1000, $ 2000, $ 2250, $ 3500 and $ 1030.
Click here to enlarge
[next page]
|
