|
Example The mean weight of 98 students is
found to be 50 lbs. It is later discovered that the frequency of
the class interval (30- 40) was wrongly taken as 8 instead of 10.
Calculate the correct mean.
Solution:
Incorrect mean 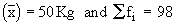
\ Incorrect 
50 = 
Therefore, Incorrect 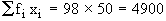
Now correct
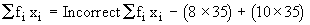
Note that the class-mark of class interval (30 - 40) is 35 and for the calculation of the mean we consider class marks.
\The correct 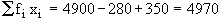
Also the correct 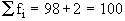
Therefore, the correct mean
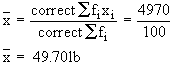
Example The sum of the deviations of 'n'
observation values of a variate from a
constant 'a', is S. Show that the arithmetic mean is 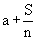 . .
Solution:
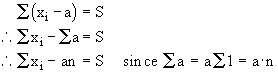
Dividing by n to get the mean
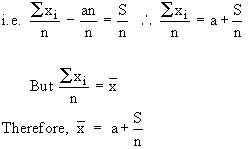
|