4.6 Empirical Relation Between Mean, Median And Mode
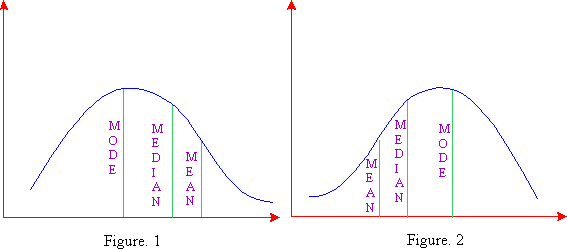
A distribution in which the values of mean, median and mode coincide (i.e. mean = median = mode) is known as a symmetrical distribution. Conversely, when values of mean, median and mode are not equal the distribution is known as asymmetrical or skewed distribution. In moderately skewed or asymmetrical distribution a very important relationship exists among these three measures of central tendency. In such distributions the distance between the mean and median is about one-third of the distance between the mean and mode, as will be clear from the diagrams 1 and 2. Karl Pearson expressed this relationship as:
Mode = mean - 3 [mean - median]
Mode = 3 median - 2 mean
and Median = mode + 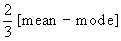
Knowing any two values, the third can be computed.
Example
Given median = 20.6, mode = 26 Find mean.
Solution:
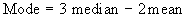
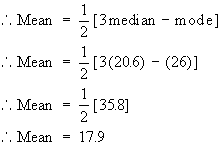
 Click here to enlarge
Click here to enlarge
**********
|