Example Find the arithmetic mean for the following :
Marks below : 10 20 30 40 50 60 70 80
No. of students : 15 35 60 84 96 127 198 250
Solution:
First, we have to convert the cumulative frequencies into frequencies of the respective classes.
|
Marks |
Mid-values
xi |
Frequencies
c.f. f.
|
U = X -A
A = 45 |
fiui
|
|
0 - 10 |
5 |
15 15
|
- 40 |
- 600 |
|
10 -20 |
15 |
35
20
|
- 30 |
- 600 |
|
20 - 30 |
25 |
60 25 |
- 20 |
- 500 |
|
30 - 40 |
35 |
84 24
|
- 10 |
- 240 |
|
40 - 50 |
45 Þ A |
96 12
|
0 |
0 |
|
50 - 60 |
55 |
127 31
|
+10 |
+310 |
|
60 - 70 |
65 |
198 71 |
+20 |
+1420 |
|
70 - 80
|
75 |
250 52 |
+30 |
+1560 |
|
Total |
|
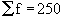
|
|
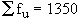 |

Step-Deviation Method
Here all class intervals are of the same width say 'c'. This method is employed in place of the Short-cut method. We measure all the class-marks (mid values) from some convenient value, say 'A', which generally should be taken as the class-mark of a class of maximum frequency or of a class which is the middle one. All the class marks happen to be multiples of c, since all class intervals are equal. We consider class frequencies as if they are centered at the corresponding class-marks.
Theorem
If x1, x2 , x3, ......, xn are n values of the class marks with frequencies f1, f2 , f3, ......fn respectively and if each xi is expressed in terms of the new variable ui by the relation xi = A + cui then, with the usual notation, we have 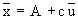
where  and and 
This method is also known as the "Coding method."
|