i) Geometrically it can be seen that the area of a sector of a circle taken radially, is proportional to the angle at its center. It is therefore sufficient to draw angles at the center, proportional to the original figures. This will make the areas of the sector proportional to the basic figures.

For example, let the total be 1000 and one of the component be 200, then the angle will be

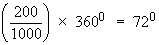
In general, angle of sector at the center corresponding to a component
           

ii) When a statistical phenomenon is composed of different components which are numerous (say four or more components), bar charts are not suitable to represent them because, under this situation, they become very complex and their visual impressions are questioned. A pie diagram is suitable for such situations. It is a circular diagram which is a circle (pie) divided by the radii, into sectors ( like slices of a cake or pie ). The area of a sector is proportional to the size of each component.

iii) As an example consider the yearly expenditure of a Mr. Ted, a college undergraduate.

Now as explained above, we calculate the angles corresponding to various items (components).

Tuition fees                 =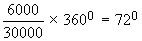  

Book and lab             =  

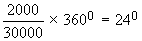
Clothes / cleaning       =  

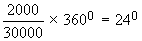
Room and boarding    =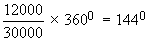  

Transportation            =  

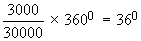
Insurance                   =  

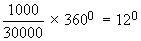
Sundry expenses       =  

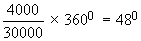
Index

3.1 Introduction
3.2 Comparison Between Tabular And Diagrammatic Presentation
3.3 Difference Between Diagrams And Graphs
3.4 General Principles Of Constructing Diagrams
3.5 Bar Diagrams
3.6 Pie Chart
3.7 Graphs
3.8 Box and Whiskers

Chapter 4