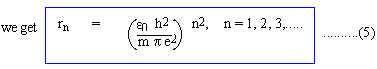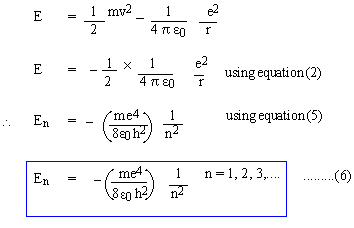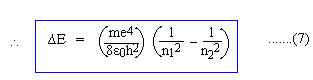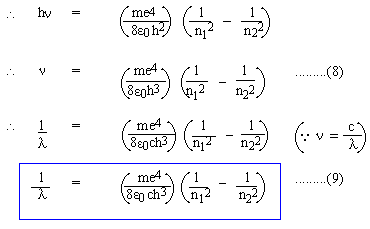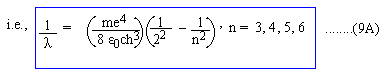The Bohr theory of hydrogen atom spectrum
From Equations (2) and (3) by eliminating v,
Thus electrons can orbit in circles of radius
:r0, 4r0, 9r0, 16r0, ......... where r =
 , the electron m
p e2 is prohibited from occupying the intervening space between these orbits.
The energy E of an electron in any 'stationary' orbit must be,
Equations (5) and (6) represent the quantized orbits and the energy of electrons in 'stationary' orbits.
Now, let an electron jump from a higher orbit n2 to a lower orbit
n1 (n2 and n1 are natural numbers; n2 > n1), then the energy lost by the electron is given by,
DE = En2 -
En1
But, according to Equation (4),
DE = hn
For a visible spectrum: n1 = 2, n2 = 3, 4, 5, 6,.....
Comparing (9A) with (1), we must have
When R.H.S is calculated it precisely turns out to be 1.097
´ 107 m-1 (!)
[next page]
|
Index
32 : Bohr's theory of hydrogen
atom and its spectrum
Chapter
33
|
