|
In figure 7.15 l and m are secants. l
and m intersect at O outside the circle. The intercepted arcs are
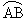 and and  . .
Ð COD
= ( m 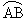 - m
- m  ) )
Figure 7.15
Conclusion :
(a) If two chords intersect in a circle the angle formed is half the sum of the measures of the intercepted arcs.
(b) Angle formed by a tangent and a chord intersecting at the point of tangency is half the measure of the intercepted arcs.
(c) Angle formed by two secants intersecting outside the circle is half the difference of the measures of the intercepted arcs.
Example 1
In the above figure seg.AB and seg.CD are two chords
intersecting at X such that m Ð
AXD = 1150
and m (arc CB) = 450
. Find m arc APD.
Solution:
m arc APD = 1850
m Ð AXD =
 { m (arc
APD) + m (arc CB) } { m (arc
APD) + m (arc CB) }
m ( arc APD) = 2 m Ð
AXD - m (arc CB)
= 2 ´
1150
-
450
= 1850
Example 2
l
is a tangent to the circle at B. Seg. AB is a chord such that m
Ð
ABC = 500.
Find the m (arc AB).
Solution:
m (arc AB) = 1000
m Ð ABC =
 m (arc
AB) m (arc
AB)
50 =  m (arc AB) m (arc AB)
m (arc AB) = 1000
Example 3
l and m are secants to the circle
intersecting each other at A. The intercepted arcs are arc PQ and
arc RS if m Ð
PAQ = 250
and m Ð
ROS = 800
find m (arc PQ).
Solution:
m ( arc PQ) = 300
m Ð PAQ =  { m (arc RS) - m (arc PQ)
{ m (arc RS) - m (arc PQ)
2 m Ð PAQ = m (arc
RS) - m (arc PQ)
\ m (arc PQ) = m (arc RS)
- 2 m Ð PAQ
= 800
- 500
= 300
|