7.4 Inscribed angles
Whereas central angles are formed by radii, inscribed angles are formed by chords. As shown in figure 8.5 the vertex o of the inscribed angle AOB is on the circle. The minor arc 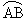 cut on the circle by an inscribed angle is called as the intercepted arc.
Figure 7.5
Theorem: The measure of an inscribed angle is half the measure of its intercepted arc.
Proof: For a circle with center O Ð
BAC is the inscribed angle and arc BXC is the intercepted arc. To
prove that m Ð BAC
= 1/2 m (arc BXC). There arise three cases as shown in figure 8.6
(a), 8.6 (b) and 8.6 (c).
Figure 7.6 (a) Figure 7.6 (b) Figure 7.6 (c)
Case 1: The center is on the angle figure 7.6 (a) join c to O.
D OAC is
an isosceles triangle as seg.OA = seg.OC.
Assume m Ð
OAC = m Ð OCA = P
m Ð
COA = 180 - 2 P as sum of all the angles of a triangle is 1800.
Ð
COA & Ð COB form
a linear pair. Therefore they are supplementary.
m Ð
COB = 1800
- m Ð COA
= 1800
-
( 1800 -
2P)
= 2P
= 2
m Ð BAC
But m Ð
BAC = m (arc BXC)
\
m Ð BAC = 
m (arc BXC)
Case 2: Figure 7.6 (b). The center is in the interior of the angle. in this case let D be the other end point of the diameter drawn through A.
Let arc CMD be intercepted by Ð
CAD and let arc Ð
BND be that which is intercepted by Ð
DAB.
From case 1 m Ð
CAD = m
( arc CMD)
and m Ð DAB =
m (arc BND)
m Ð
CAD + m Ð DAB =
m (arc CMD) +
m (arc BND)
m Ð BAC =
{ m ( arc CMD) + m (arc BND) }
=
m (arc BXC)
Case 3: The center is in the exterior
of the angle. Again let D be the other end point of the diameter
drawn through A. Let arc CMD be the one intercepted by Ð
CAD and let arc BND be the one intercepted by Ð
DAB.
From case 1 m Ð
CAD =
m (arc CMD)
m Ð
DAB =
m (arc BND)
m Ð
CAD - m Ð DAB =
m (arc CMD) -
m (arc BND)
m Ð
CAB = {
M (arc CMD) - m (arc BND) }
= m (arc BXC)
|
