6.3 Special Right Triangles
The 300 - 600 - 900
triangle : If the angles of a triangle are 300
, 600 and 900 then the side
opposite to 300 is half the hypotenuse and the
side opposite to 600 is 
times the hypotenuse.
Figure 6.5
In D ABC Ð
A = 900 Ð B = 600
and Ð C = 300
To prove that l
(AB) = 
l (BC) and l
(AC) =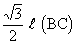 
Take a point D on ray BA such that seg.AD @
seg.AB and join CD.
In D ABC and D
ACD
AB @ AD construction
Ð CAB @ Ð
CAD both are right angles
AC @ AC common side
\ D BAC @ D
DAC (SAS)
\ Ð ACB @
Ð ACD corresponding angles of congruent triangles are
equal.
but m Ð ACB = 300
\ m Ð
DCB = 600
Þ D DCB is an equilateral triangle
\ l
(seg.DC) = l (seg.BC) = l
(seg.DB) ® (1)
but l (seg. AB) =
l (DB) ® (2)
®(3) from (1) and (2).
In right triangle ABC
l (seg.AB)2 + l
(seg.AC)2 = l (seg.BC)2 Pythagoras
{ 
l (seg.BC)2 } + l
(seg.AC)2 = l (seg.BC)2from
(3)
l (seg.AC)2 = l
(seg.BC)2 -
l (seg.BC)2
= 
l (BC)2
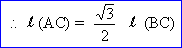
The 450 - 450 - 900 triangle
: If the angles of a triangle are 450 - 450
- 900 then the perpendicular sides are 
times the hypotenuse.
In D ABC Ð
A = 450 , Ð B = 900
and Ð C = 450.
Figure 6.6
To prove that AB = BC =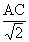 
By Pythagoras theorem
l (seg.AB)2 + l
(seg.BC)2 = l (seg.AC)2
l (seg.AB) = l
(seg.BC) . D ABC is isosceles.
\ l
(seg.AB)2 + l (seg.BC)2
= 2 l (seg.AB)2 =
l (seg.AC)2
 
|
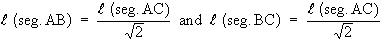
