Theorem : If two angles are complementary
to equal angles they are equal to each other . If Ð
a and Ð
b are complementary to Ð
c and Ð
d respectively where m Ð
c = m Ð d.
Proof : m Ð
a + m Ð
c = m Ð
b + m Ð
d = 900
m Ð a + m Ð c = m Ð b + m Ð d
Since m Ð c = m Ð d
m Ð a + m Ð c = m Ð b + m Ð c
or m Ð a = m Ð b.
Supplementary angles :
If the measures of two angles sum up to 1800
they are called supplementary angles. Supplementary angles are of
two types :
a) Non adjacent supplementary angles and
b) Adjacent supplementary angles.
Non adjacent supplementary angles are distinct and have no arm in common (figure 1.21).
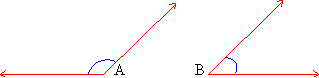
Figure 1.21
Ð A and Ð B are supplementary
and non adjacent.
Adjacent supplementary angles are called angles in a linear pair and have one
arm in common ( figure 1.22 ).
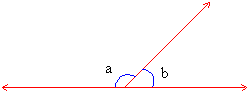
Figure 1.22
Vertical angles : When two lines AB and
CD intersect at O, four angles are formed with vertex O. Consider
Ð AOC and Ð
BOD. It is observed that 
and  are
opposite rays and so is 
and 
. In such a case Ð AOC and Ð
BOD are called vertical angles ( figure 1.23 ).
Figure 1.23
|
