1.5 Angles made by a transversal
Definition of a transversal : A line which
intersects two or more given coplanar lines in distinct points is
called a transversal of the given lines. In figure 1.24 the line
l is the transversal of lines a and b.
Figure 1.24
l intersects a and b at P and Q respectively.
The three lines determine eight angles four with vertex P and the
remaining four with vertex Q.
Corresponding angles : Angles that appear in the same
relative position in each group are called corresponding angles,
i.e. Ð 1 and Ð
5 are called corresponding angles. Similarly Ð
2 & Ð 6, Ð
4 & Ð 8 and Ð
3 & Ð 7 are pairs of corresponding
angles.
Interior and Exterior angles : Those angles
which lie between lines a and b are called interior angles, i.e.
Ð 3, Ð 4,
Ð 5 and
Ð 6 . Exterior angles lie on opposite
sides of lines a and b, i.e. Ð 1, Ð2,
Ð 7 and Ð 8 .
Alternate and Consecutive Interior angles :
Interior angles on opposite sides of the transversal are called
alternate interior angles and Ð 4,
Ð 6 are alternate interior angles
and so also Ð 3, and Ð
5 .
Interior angles on same side of the transversal are called
consecutive interior angles. Ð 4,
and Ð 5 are consecutive interior
angles and so also Ð 3
and Ð 6 .
Alternate and Consecutive Exterior angles :
Alternate exterior angles are on opposite sides of the transversal
and do not lie between lines a and b, i.e. Ð
1 and Ð 7 and also Ð
2 and Ð
8 .
Exterior angles on the same side of the transversal are called consecutive exterior angles, i.e. Ð 1 & Ð 8 as also Ð 2 and Ð 7 .
Example 1
In figure 1.25 n is the transversal of lines l and m. Write down the pairs of :
a) corresponding angles ,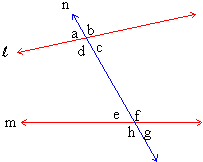
b) alternate interior angles,
c) alternate exterior angles ,
d) consecutive interior angles & ,
e) consecutive exterior angles.
Figure 1.25
Answers
a) Ð a & Ðe , Ð
b & Ð f , Ð c & Ð g , Ð d & Ð h .
b) Ð d &
f , Ð c & Ð
e
c) Ð a & Ð g , Ð b & Ð h
d) Ð f & Ð c , Ð d & Ð e
e) Ð a & Ð h , Ð b & Ð g .
|