|

Figure 1.2
Figure 1.2 shows two lines l and m . Line l is such that it passes through A, B and C. Hence points A B and C are collinear. In the case of points P, Q and R there can be no single line containing all three of them hence they are called non-linear.
Similarly points and lines which lie in the same plane are called coplanar otherwise they are called non-coplanar.
Axiom : A plane containing a line and a
point outside it or by using the definition of a line, a plane can
be said to contain three non-collinear points. Conversely, through
any three non collinear points there can be one and only one plane
(figure 1.3).
Axiom : If two lines intersect, exactly
one plane passes through both of them (figure1.4).
Axiom : If two planes intersect their intersection
is exactly one line (figure 1.5).
Figure 1.3
Lines A, B and C are contained in the same plane P or A, B and C are three non-collinear points through which one plain P can pass.
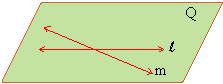
1.4
Plane Q contains intersecting lines l and m .

Figure 1.5
Planes P and Q intersect and their intersection is line l .
|