(Equimarginal utility = 82, Total budget = $10)

With the rise in the price of good X and the price of good Y remaining constant a new equilibrium position has been established. In this equilibrium position, the consumer reduces the consumption of good X, which has become ’dearer’. Instead of 2 units, only 1 unit of X is purchased and $6 are spent on good X. The remaining $4 are now spent on purchasing two units of good Y. Once again the Mu/P ratio for the two goods has been equated with its value ’8’ for the new combination. The consumer who is continually maximizing his utility keeps on making such readjustments whenever the market price of goods changes.

(E) Substitution Principle: The law of equimarginal utility as the basis of consumer equilibrium can be extended to cover any number of goods. In its general form, the law can be stated as

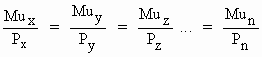
This law is also known as the principle of substitution. In order to maximize satisfaction the law requires the substitution of units of one good in place of the other so long as the ratio is not brought into equality. This can be illustrated with the help of two goods. Let us begin with an initial equilibrium position of Mux = 8, Px = 4, Muy = 12 and Py = 6,

If the price of X falls to $2 and the price of Y is constant then,

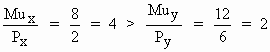
Therefore the Mu/P ratio for good X whose price has fallen is now greater than the similar ratio for good Y whose price has not fallen. According to the rule, there will be an increase in the consumption of the cheaper good (X) and a decrease in the consumption of the dearer good (Y).

With every increase in the units of good X consumed, the marginal utility for good X (Mux) will start falling. And with every decrease in the good Y consumed Muy will start rising. Continue the process until the two ratios are equated. If price of X remains constant but that of Y falls then the value of the first ratio will be smaller than that of the second. In this case an increase in the consumption of Y and a decrease in the consumption of X will help to reestablish the equilibrium. This principle of substitution is the basis of consumer equilibrium. We will later study a golden rule based on the principle of substitution.

(F) Substitution and Income effects: Marginal utility, equimarginal utility or law of demand in general, help to analyze consumer behavior. Price and the quantity of a good are generally inversely related. This means that the consumption or demand of a good increases if its price falls and the consumption or demand of a good decreases if its price rises. There are two distinct effects that underlie such an inverse tendency. They are known as substitution and income effects. Substitution effect means the tendency of a consumer to reduce the consumption of a relatively dearer good and to increase the consumption of a relatively cheaper good. As a result of this, the consumption or demand of a good whose price has fallen, increases. For example: let a consumer spend a total amount of $10 in equal proportion of $5 each on two brands of soap. Both varieties of soap perform the same function and therefore are substitutes of each other. If the price of one of the brands falls, it becomes cheaper. The consumer may then spend more (say $7) on it and increase the demand for the cheaper brand?. On the other hand, he is left with only $3 which he spends on the second brand. The demand for the second brand which is relatively dearer, therefore decreases. Such an act of shifting demand from a dearer to a cheaper good is called the substitution effect. This kind of an effect works in the inverse direction: a fall in price results in a rise in demand and is therefore negative in its influence.

There is another cause for increase in demand of a good of which price falls. It is in the form of an income effect. As a result of a fall in the price of a commodity, a consumer becomes ’richer’ and his income increases. Let us suppose that a consumer has a sum of $12 to spend on a certain good, the price of which is $4 per unit. With his income he can purchase 3 units of the good. When the price of the good falls from $4 to $3 and if he continues to buy 3 units as before then $9 would be enough. He is now left with $3 of ’additional’ allowance. This is the income effect. If he decides to spend these additional $3 on the same good his total demand will increase from 3 to 4 units. The income effect further enables a consumer to increase his demand for cheaper goods. Note that a rise or fall that occurs with a change in the price of a good is not an increase in the money income of a consumer (which is constant as $12) but it is an increase in the real income of a consumer. Since an increase in income and an increase in consumption are changes in the same direction, the income effect is said to be direct and positive. The income effect is generally positive for ’normal’ goods. Only in the case of exceptional type of ’inferior’ goods the income effect becomes negative.

Index