Example 17 Find the volume of the solid generated by revolving the region bounded by y = log x and the x-axis on [2, 3] about the x-axis.
Solution : Here x-axis is the boundary of the region. Using the disk method,
Now f (x) = y = log x
\ The volume (V) of the solids
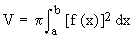
\ 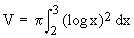
Integrating by parts, we get
V = 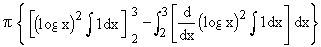
= 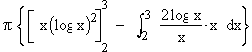
=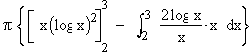
Integrating by parts, we get
V =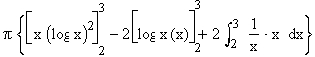
= 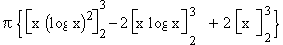
V = 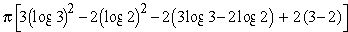
= 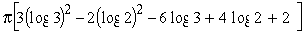
Example 18 Find the volume of the solid generated by revolving about the y-axis the area of the parabola x + y2 - 4y = 0 in the first quadrant.
Solution : Since the region has y-axis as its boundary, we can use the disk method as,
Now the parabola is x + y2 - 4y = 0 which can be
written as (y - 2)2 = 4 - x
\
Its vertex is (4, 2)
It intersects y - axis where x = 0
\
y2 - 4y = 0
\
y = 0
and y = 4 i.e. on [0, 4].
The required volume (V) of revolution about y-axis is
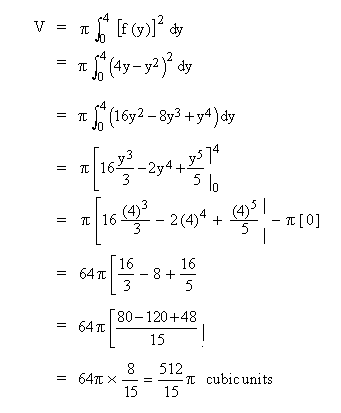
Example 19 Let the region bounded by the curves y = x2 , x = 0 and y = 1 be revolved about the y-axis. Find the volume of the solid resulting from the revolution.
Solution : Since the region has the y- axis as its boundary, we can use disk (or circular slab) method as,
[ f (y)]2 = y on [0, 1] .....(see the figure)
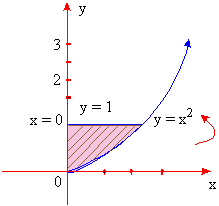
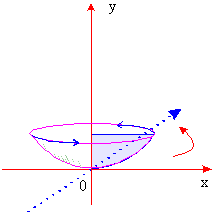
The volume (V) of the solid is
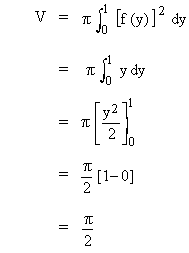
[next page]
|
Index
8.1 Introduction
8.2 Area
8.3 Volumes
8.4 Mean Value
8.5 Arc Length(Rectification)
Chapter 1
|