8.5 Arc Length ( Rectification )
The method of finding the length of the arc of a curve is called the rectification.
For arc length, the function and its derivative must both be continuous on the closed interval.
If y = f (x) and f’ (x) are continuous on [ a, b ], then the arc length ( L ) of f (x) on [ a,b ] is given by
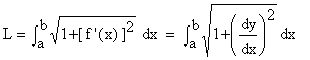
Similarly for, x = f (y) and f’ (y) are continuous on [ a,b ], then the arc length (L) of f (y) on [ a,b ] is given by
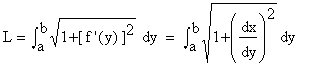
Example 29 Find the length of the arc of f (x) = x3/2 on [ 0, 5 ].
Solution :  both are continuous on [ 0, 5 ].
then length of arc of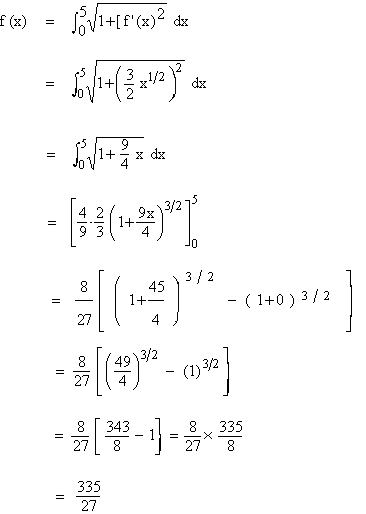 
Example 30 Find the length of the arc of the parabola y2 = 12x cut off by the Latus rectum.
Solution : y2 = 12 x ®
Parabola.
Comparing with y2 = 4 ax, we see that 4 a = 12 \
a = 3 \
AS = SL = 6 \ co-ordinates of L are (3,6)
 
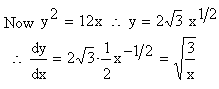
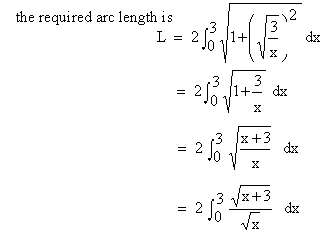
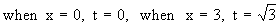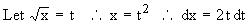
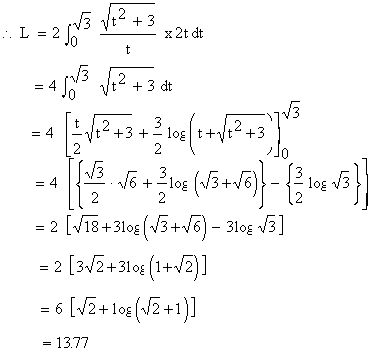
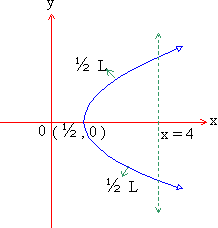
Example 31 Find the length of the curve y2 = (2 x - 1 )3, cut off by the line x = 4.
Solution : y2 = (2 x - 1 )3 is a curve
(i) symmetrical about the x-axis
(ii) not passing through (0,0)
(iii) it cuts the x-axis, where y = 0 \
x = ˝
\
It's vertex is at ( ˝ , 0)
(iv) It does not cut the y-axis as, taking x = 0
we get y = ± i
(v) No asymptotes.
(vi) (2x - 1)3 positive \
y2 ³
0
\
x ³
˝
\
The curve lies in only 1st and 4th quadrants
Now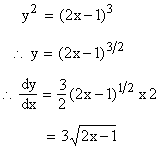 
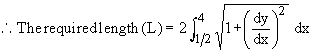
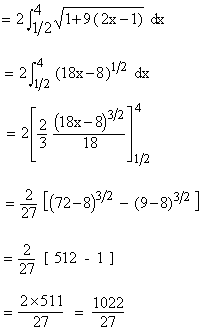
[next page]
|
