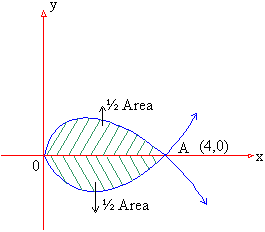
Example 6 Find the area of the loop of the curve y2 = x (4-x)2
Solution : Put y = 0 then 0 = x (4-x)2
\
x = 0 and x = 4 (twice)
The curve passes through the (0, 0) and loop has the point A (4, 0) on it. The required area
A = 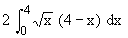
= 
= 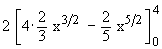
=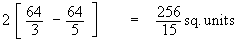
Example 7 Find the area of the region bounded by the curves y = x2 and y = 3 - 2x.
Solution : Solving y = x2 and y = 3 - 2x, we get
x2 = 3-2 x \
x2 + 2 x - 3 = 0
\ (x + 3) (x + 1) = 0
\ x = -3, x = 1
Hence the curve intersects x-axis at (-3, 0) and (2,0) since 3-2 x > x2 on [ -3, 1 ], the area of the region is given by
A = 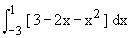
= 
\
A = 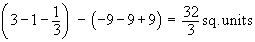

[next page]
|