|
Example 37
Evaluate 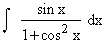
Solution : Let cos x = t
then -sin x dx = dt
\ sin x dx = -dt
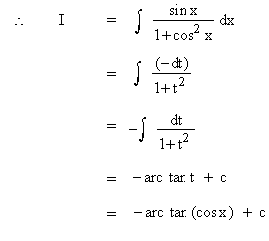
Example 38
Evaluate 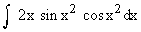
Solution : Let x2 = t
then 2x dx = dt
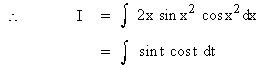
Again put sint t = u, then cos t dt = du
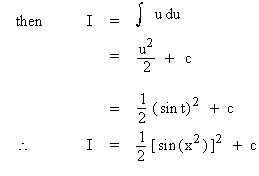
Example 39
Evaluate 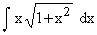
Solution : Let 1 + x2 = t
then 2x dx = dt
\ x dx = ˝ dt
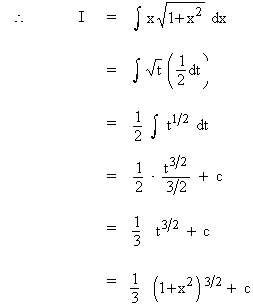
Example 40
Evaluate 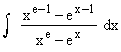
Solution : 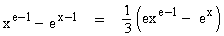
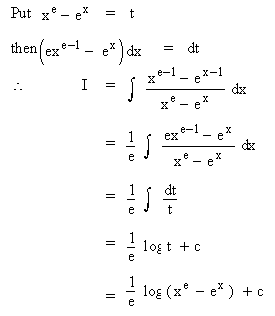
Example 41
Evaluate 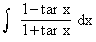
Solution :
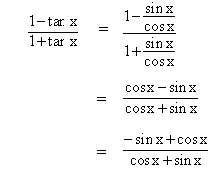
Let cos x + sin x = t then (-sin x + cos x) dx = dt
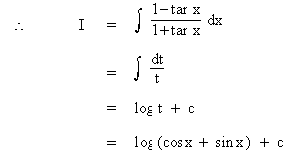
[next page]
|
Index
6.1 Anti-derivatives
(indefinite Integral)
6.2 Integration Of Some Trignometric Functions
6.3 Methods Of Integration
6.4 Substitution And Change Of Variables
6.5 Some Standard Substitutions
6.6 Integration By Parts
6.7 Integration By Partial Fractions
Chapter
7
|