|
CHAPTER 7 : DEFINITE INTEGRAL
7.1 Definition
If for any partition of [a, b] the lim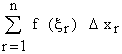
when n tends to infinity in such a
way that the largest of all the subinterval D x1 , D x2 , ......., D xn tends to zero, exists,
then the function which is continuous on [a, b] is said to be integrable over the closed
interval [a, b] and it is
denoted by  f(x) dx. .
Let f (x) be any function of x, assumed to be continuous on the closed interval [a , b].
Divide [a , b] into a finite number, say n sub-intervals (not necessarily equal) by means of points x1 , x2 , ......., xn -1 such that
a = x0 < x 1 < x 2 ........... < x n -1 < xn = b
This is called a partition of [a, b] into ’n’ sub intervals.
Let  be numbers such that
Now the subsequent function values at these numbers are f ( x1), f (x2 ), f (x3), .......,
f (xn ) respectively.
Then the products of each function value and its sub interval length are
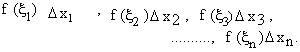
Now consider the sum
i.e. 
This sum is called as "Riemann Sum" which can be positive, negative or zero depending upon the behavior of f (x) on [a, b].
For example
If f (x)  0 on [a, b] the Sn is a positive real number.
If f (x) 0 on [a, b] then Sn is a negative real number.
Now if the number of these sub intervals increased indefinite, by the lengths of each sub interval would get smaller and smaller i.e. n ® ¥ then Dx ® 0.
Under this effect, the limit of this Riemann Sum (S n ) if exists, then f (x) is said to be integrable on [a, b]. This limit is called the definite integral of f (x) on [a , b] and is denoted by 
Thus the definite integral of f (x) from a to b is defined as
|
