| Note :
i) The word integration literally means to add together small bits. Now the question arises that is there any connection between the two meanings of integration :
(i) The Inverse of differentiation.
(ii) The Adding together of small bits.
Yes, there is such a connection between the above said two concepts. This, has been mentioned later in the fundamental theorem of Integral calculus.
ii) Also note that the constant " c " in the above discussion is known as the constant of integration.
iii) Any integral of f ( x ) is in the form f ( x ) + c. which is known as the general integral of f ( x ).
An integral obtained by giving particular value to ‘ c
’ is called a particular integral.
Some Standard Results
Given below are some standard results, obtained by using the derivatives of some well-known functions.
(1) 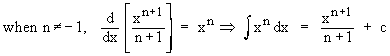
(2) 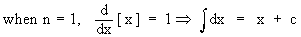
(3)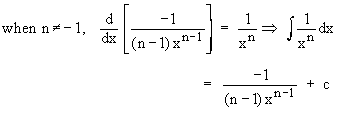
(4) 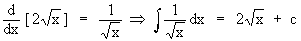
(5)
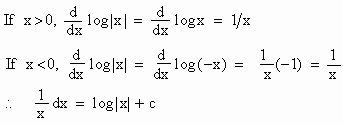
(For the sake of convenience it is customary to omit the modulus sign)
[next page]
|