|
Example 46 A car is traveling north
towards an intersection at the rate of 120 mph while a truck is
traveling east away from the intersection at the rate 100 mph. Find
the rate of change of the distance between the car and the truck
when car is 9 miles south of the intersection and the truck is 8
miles east of intersection.
Solution :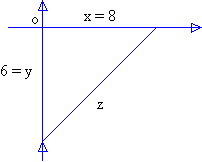 
Let x, y and z be distances, traveled the truck (east wards), the car (north wards) and between the truck and the car respectively. Also x = 8, y = 6 and z = ?
By the theorem of Pythagoras, we have
z2 = x2 + y2 Þ z2 = ( 8 )2 + ( 6 )2 = 100
\ z = 10
Differentiating w. r. to ’ t’ , we get
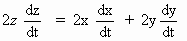
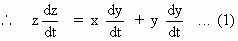
Now
= 100 mph = the rate of change of the truck
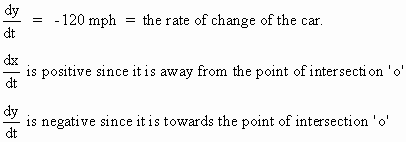
\ (8)
(100) + (6) (-120) = (10)  ...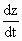
(By 1)
\ 800
-720 = 10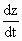
\ 80
= 10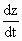
\
=
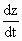8
\ The distance between the car and the truck is increasing at a rate of 8 mph.
[next page]
|
