|
Example 43
A
man of height 180 cm is moving away form a lamp-post at the rate
of 1.2/sec. If the height of the lamp-post is 4.5 m. Find the rate
at which the shadow is lengthening by the rate at which its tip
is moving away from the lamp-post.?
Solution :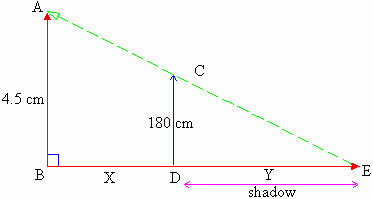
AB = lamp-post,
AB = 4.5 cm
CD = Man.
CD = 180 cm =1.8 m
DE = Shadow
and distance of the tip E of the shadow from the
pole = BE
Let BD = X and DE = Y
then BE = X + Y
Now D ABE ~ D CDE ... (By AA test for similar triangles)
\ 
\ 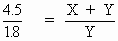
\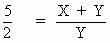
\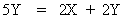
\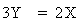
\ 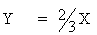
Differentiating w. r. to ’ t ’.
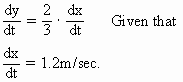
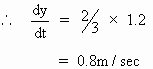
\ The
shadow is lengthening at the rate 0.8 m / sec.
Also BE = X + Y
\ Differentiating w. r. to ’ t’
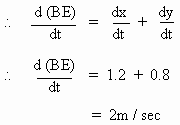
\ The rate at which
the tip of the shadow is moving away from the lamp-post is 2 m/sec.
[next page]
|