|
Example 18
If f (x) = x4 - 8x2, determine
all local extrema (maxima and minima) for the function.
Solution : f (x) = x4
- 8x2
\ f '(x) = 4x3
- 16x
For critical points (i.e. roots of f ' (x)
) f ' (x) = 0 Þ
4x3 - 16x = 0 or
4x (x2 - 4) = 0 or
x = 0, x = -2, x = 2
Now for h > 0 (very small)
f ' (0 - h) = 4 (0 + h)3 - 16 (0 - h) = 4h3 + 16h > 0
and f'(0+h) = 4 (0 + h)3 - 16 (0 + h) = 4h3 + 24h2 + 32h >0
i.e.f'(x) changes its sign from negative to positive around x =-2
\ f ' (x) has a Local minimum at
x = -2 i.e. (-2, -16)
Similarly we can show that f '(2 - h) < 0 and f ' (2 + h) > 0
\ f '(x)
changes its sign from negative to positive around x = 2
\ f '(x) has a local minimum
at x = 2
i.e. (2, -16)
Example 19
Find the maximum and minimum values of f (x)
= 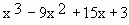
Solution : f (x) = 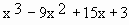
\ f ' (x) = 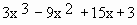
\ f '(x) = 
= 3 (x - 5) (x - 1)
For critical points of f (x), f ' (x) = 0 Þ
x = 5 and x = 1
Now 1 - nbd of 5 we have
f ' (x) < 0 when x < 5
f ' (x) > 0 when x > 1
\ f (5) is a
minimum value and f(5) = - 22
\ f (1) is maximum
value and f(1) = 10

Next in 1 - nbd of 1, we have
f ' (x) > 0 when x < 1
f ' (x) < 0 when x > 1
\ f (1) is maximum value and f (1) = 10

[next page]
|