|
Example 9
Show that f (x) =  is decreasing in
is decreasing in  and increasing in
and increasing in 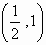
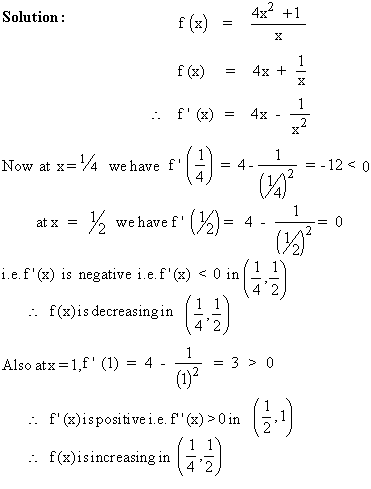
Example 10
For 0 < x < 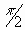 ,
show that sin x < x < tan x ,
show that sin x < x < tan x
Solution : I) Consider the
part, sin x < x of the inequality
sin x < x < tan x for
0 < x < 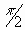
consider f (x) = x - sin x
\ f ' (x) = 1 - cos x
Now for 0 < x < 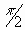 , cos x < 1 Þ ( 1 - cox ) >
0
, cos x < 1 Þ ( 1 - cox ) >
0
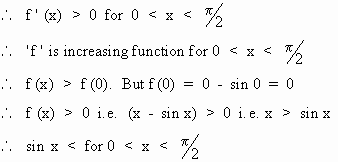
II) Consider x < tan x for 0 < x <
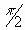
Let g (x) = tan x - x \
g' (x) = sec2 x - 1 = tan2
x
For 0 < x < 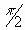 , tan2 x > 0 \g' (x) >
0
, tan2 x > 0 \g' (x) >
0

Hence from (I) and (II), we get sin x < x < tan x for 0 <
x < 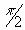
[next page]
|