|
Illustrative Examples:
Example 1 Discuss the following functions for continuity
i) f (x) =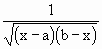
ii) f (x) =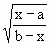 
Solution : i) f (x) = .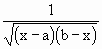
Here f (x) is continuous for all x for which a < x< b if b > a and b < x < a if a >
b. The denominator becomes 0 when x = a and x = b.
\ The function is discontinuous at x = a and x = b
ii) f(x) =  .
In this case ’f’ is continuous for all x for which a < x £
b if b > a and continuous for all x for which b £
x < a if a > b. It is discontinuous at x = b which makes the
denominator zero.
Example 2 Discuss the continuity of y = [x] where [x] denotes the positive integer in x not greater than x.
The graph of the function is shown in the figure. This graph
consists of portion of the portions of the line defined in the domains as under
y = 0 for 0 £ x < 1
y = 1 for 1 £ x < 2
y = 2 for 2 £ x < 3
y = -1 for -1 £ x < 0 and so on
i.e. for any integer n. [x] is continuous from the right only
because f(n) = [n] = n.
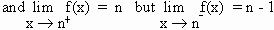
is not continuous at n from left.
Thus f(x) is continuous for all x except for x = 1, 2, 3, ......
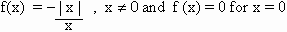
Example 3 Discuss the continuity of
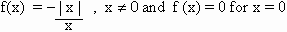
Solution : This can be written as
f(x) = 1, x > 0
f(x) = 0, x = 0
f(x) = -1, x < 0
Graphically f(x) is discontinuous at x = 0
Analytically
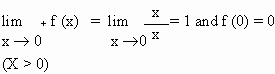
Hence the function is discontinuous at this point.
[next page]
|
