Example 4 A function f(x) is given as follows

f(x) = for x < 1

f(1) = 3

Examine the continuity of f(x) in (-3, 3)

Solution : f(x) = in (-3, 1) since x < 1

Now f(-2) is not defined as denominator is 0 for x = -2

since x = - 2 Î (- 3, 1) \ f(x) is discontinuous at x = -2 in (-3, 1)

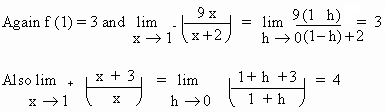
Since the right hand and left hand values of f(x) at x = 1 are not equal,

therefore f(x) is discontinuous at x = 1.

Summing up we have the following results

f(x) is discontinuous at x = -2 and 1. For all other values of x it is continuous.

Example 5

Discuss the continuity of the function x - [x] with the help of its graph.

Solution : In the domain 0 £ x < 1 , [x] = 0

Let us assign to x, the values 0.12, 0.23, 0.34, 0.45 .......

then f(0.12) = 0.12 - [0.12] = 0.12 - 0 = 0.12

f(0.23) = 0.23 - [0.23] = 0.23 - 0 = 0.23

similarly f(0.34) = 0.34 and f(0.45) = 0.45,....... and so on.

The graph for 0 £ x < 1 is segment OA1

Again if we assign x, the values 1, 1.1, 1.2, 1.3, 1.4......

in 1 £ x < 2 then f (11) = 1 - [11] = 1 - 1 = 0

f(1.1) = 1.1 - [1.1] = 1.1 - 1 = 0.1

f(1.2) = 1.2 - [1.2] = 1.2 - 1 = 0.2

f(1.3) = 1.3 - [1.3] = 1.3 - 1 = 0.3 and so on.

Then segment B₁A₂ which is parallel OA₁. Similarly the graph consists of bits of parallel lines B₂A₃, B₃A₄......From the graph, it is quite clear that points 0, ±1, ±2, ± 3,.... are points of discontinuity.

[next page]

Index

3.1 Continuity At a Point
3.2 Continuity In An Interval
3.3 Some Very -often - encountered Continuous Functions
3.4 Algebra Of Continuous Functions
3.5 Discontinuity And its Classification
3.6 Properties of Functions Continuous on an Interval

Chapter 4