|
Note that in discussing maxima and minima, it can be shown that the box will have largest possible volume when x = 2 cm.
Example 9 A piece of wire 90 cm long is
cut at a distance of x cm from its one end and then bent the two
pieces into two squares. Find the formula for the total area A of
the two squares as a function of x.

Solution :
The length of the wire is 90 cm
Let the length of the 1st piece be x cm,
then the length of the 2nd piece will be (90 -x) cm
Using Area of a square = (side)2,
We have the total area of the two squares
given by A = Area of 1st square + Area of the IInd square
i.e. A = 
i.e. A =  = = 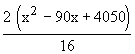
i.e. A =  sq. cm. sq. cm.
Example 10 A travel agency offers a tour. It charges
$20 per person if fewer than 25 people go. If 25 or more people,
upto a maximum of 110, take the tour, they charge $ 22.40 less 10
cents times (per person) the number of people who go. Find the formulas
which express the total charge C as a function of number x who go.
Include the domain of each formula.
Solution : Let x be the number of people go. Then 0 £ x £ 110
The formula is Total charge (C) = (Charge per person) ´ (number of people)
If fewer than 25 people go, the charge per person is $20 so that the total charge is y = 20x
If 25 people or more go, then the charge per person is $ 22.40 less 10 cents times the number of people who go .
\ The total charge in this case is y = (22.40 - 0.10x)x
so altogether the rule is
C = { 20x 0 £ x < 25 }
= { (22.40 - 0.10x ) x}, 25 £ x £ 10
|