|
(3) h(x)= x2- 6x + 7 = x2 - 6x + 9 - 9 + 7 = (x - 3) 2 - 2
(Note this !)
Since x Î R , (x - 3) Î R Þ (x - 3)2 ³ 0 Þ (x - 5)2 - 2 ³ 0 - 2
\ h (x) ³ - 2. This is the range of 'h'.
Example 5 Find the largest possible set of real numbers which can be the domain of
f(x) = 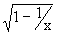
Solution : Since 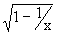 is defined only when is defined only when 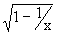 ³ 0 ³ 0
i.e. f(x) is defined for 1 -  ³ 0 ³ 0
i.e. f(x) =  ³ 0 Setting numerator and denominator separately equal to zero ³ 0 Setting numerator and denominator separately equal to zero
and solving, we get x = 0 and x = 1 (cut points)
|
Interval |
Test value |
value of f (x) |
sign of f (x) |
|
(- ¥, 0) |
-1 |
+2 |
+ |
|
(0, 1) |
½ |
- ½ ½ = -1 |
- |
|
(1, ¥) |
2 |
½ |
+ |
Graph of expression of f(x) > 0 
Graph of expression of f(x) ³ 0 
\ The domain is the set = { x | x < 0 or
x ³ 1 } = ( - ¥
, 0) È [1, ¥)
Example 6
If f (x) = x + 5 and t = 5 + 4x
3x
- 4 3x
- 1
then show that f (t) = x
Solution :
f(x) = x + 5 \ f(t) = t + 5 putting t = 5 + 4x
3x - 4 3t - 4 3x - 1


\ f(t) = 19x = x \ f (t) = x
19
|