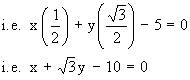| Example Find the equation of a straight line, whose normal from the origin has length 5 units and inclination with positive of x-axis is 600. Solution : Inclination a = 600 and length of normal p = 5 units. Using x cos a + y sin a = p , the equation of the line will be x cos 600 + y sin 600 = 5
Example If the graph of the linear function f is parallel to 3x + 2y + 1 = 0 and f (0) = 4, find f (x). Solution : 3x + 2y + 1 = 0 is a straight line and f (x) is a linear function parallel to 3x + 2y + 1 = 0 then f (x) must be in the form 3x + 2y + k = 0 where k will be determine by f (0) = 4 i.e. when x = 0, y = 4. Now inserting x = 0 and y = 4 in 3x + 2y + k = 0, we get 3 (0) + 2 (4) + k = 0 \ k = -8 \ 3x + 2y + k = 0 will be 3x + 2y - 8 = 0 i.e. 2y = - 3x + 8 y = i.e. f (x) = Example If the graph of the linear function G is perpendicular to 3x - 4y + 2 = 0 and G (0) = - 3, find G (x). Solution : 3x - 4y + 2 = 0 is a straight line and G (x) is also a linear function perpendicular to 3x - 4y + 2 = 0 then G (x) must be in the form 4x + 3y + k = 0 where k will be determined by G (0) = -3 . i.e. when x = 0, y = -3 Inserting x = 0 and y = - 3 in 4x + 3y + k = 0, we get 4 (0) + 3 (-3) + k = 0 i.e. k = 9 \ we have 4x + 3y + 9 = 0 i.e. 3y = - 4x - 9 i.e. y = i.e. G (x) =
|
8.1 Definition |