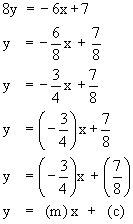We say that the line y = mx + c intersects the y - axis, at the point (0,C) Justification: any point on the y - axis has x - coordinate = 0. Since the line crosses y - axis, the point of intersection of the line y = mx + c and y - axis has x - co-ordinate = 0 putting x = 0 in y = mx + c we get y = c.

Now we can say that the line y = mx + c makes an intercept c on the y-aixs. Hence for finding an intercept made on the y - axis by any line, we must put x = 0 in the equation and find y.

Similarly for finding x - intercept of a line put y = 0 in the equation of the line and find x.

Example Find the intercept made by the line 2y - 3x = 7 on both the coordinate axes.

Solution :

1. Putting x = 0 in 2y - 3x = 7 we get 2y = 7

   \ y = 7/2

   which means the line makes an intercept 7/2 on the y-axis

2. Putting y = 0 in 2y - 3x = 7 we get -3x = 7

   \ x = -7/3

   Which mean the line makes an intercept -7/3 on the x - axis.

Any straight line expressed in this form always takes the form y = mx + c where m stands for the slope and c stands for the y - intercept of the line which involves two relationships.

1. The slope
2. The intercept i.e. the point at which the line crosses the y - axis. When an equation is put in the form y = mx + c it is said to be in y - form or slope - intercept form.

Example State the slope and y - intercept of the straight line y = -x + 7

Solution :    y = -x + 7 comparing it with y - form as

Example    Show that the lines given by 3x + 4y -3 = 0 and 6x + 8y -7 = 0 are parallel.

Solution : Ist line is 3x + 4y - 3 = 0

Putting in y - form, we get,

Therefore slope m₁ = -3/4

Also, the second line is 6x + 8y -7 = 0

putting in y - form, we get,

Therefore, slope m₂ = -3/4

Since m₁ = m₂, the two lines are parallel

Thus when an equation is put in the form y = mx + c

i.e. y - form, it should be evident that the slope is the same as the coefficient of x term.

Index

8.1 Definition
8.2 Relations, Graphs and Symmetry
8.3 Slopes and Intercepts

Chapter 9