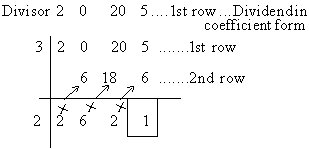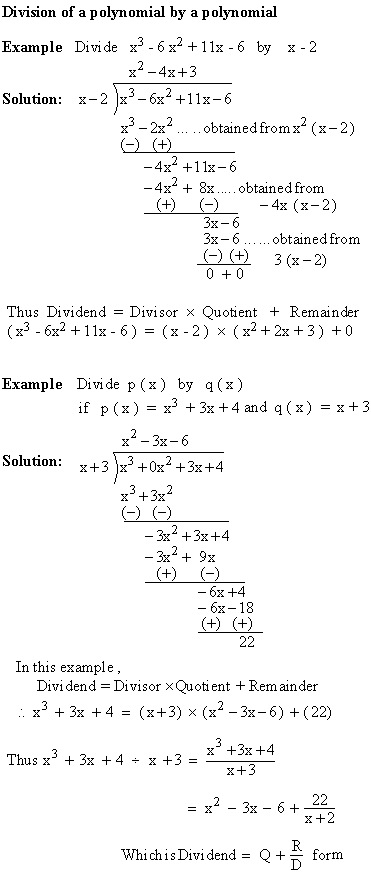
Coefficient form: Consider x3 + 3x5 + 6 + x + x2 . We write it in the standard form i.e. descending powers of x as 3x5 + x3 + x2 + x + 6. In this form the term containing x4 is mission. We insert this missing term and write it as 3x5 + 0x4 + x3 + x2 + x + 6 ....... (1) Now we express this as ( 3, 0, 1, 1, 1, 6 ). This form is known as the "coefficient form" of the polynomial and the polynomial in (1) is in its index form. Note : If the degree of the polynomial is n then its coefficient form has n + 1 terms in ( ....). In above example n = 5 \ there are 5 + 1 = 6 terms in coefficient form. Example Express the following in their coefficient form a) 7x5 + x - 9 b) x3 + x2 - 1 c) x2 + x - 3 d) x6 - 1 e) x f) 7 Solution: a) 7x5 + x - 9 ® degree n = 5
7x5 + 0 x4 + 0x3 + 0x2 + x - 9 \ Its coefficient form is ( 7, 0, 0, 0, 1, -9 ) b) x3 + x2 - 1 ® degree n = 3 \ Index form : x3+ x2 + 0x - 1 \ Coefficient form : ( 1, 1, 0, -1 ) c) x2 + x - 3 \ Index form : x2 + x - 3 \ Coefficient form : ( 1, 1, -5 ) d) x6 - 1 \ Index form : x6+0x5+0x4+0 x3 + 0x2 +0 x - 1 \ Coefficient form : ( 1, 0, 0, 0, 0, 0, -1 ) e) x \ Index form : x + 0 \ Coefficient form : ( 1, 0 ) f) 7 \ Index form : 7 x0 \ Coefficient form : ( 7) Example Express in the index form in ‘ x ’ a) ( 2, -1, 4, 0 ) b) ( 3, 0, 0, 1 ) c) (1, 0, 0, 0, 1) Soltuion: a) Coefficient form : ( 2, -1, 4, 0 ) Þ n + 1 = 4 \ n = 3 \ Index form : 2x3 - x2 + 4x + 0 = 2x3 - x2 + 4x
b) Coefficient form : ( 3, 0, 0, 1 ) Þ n + 1 = 4 \ n = 3 \ Index form : 3x3 - 0x2 + 0x + 1 i.e. 3x3 + 1 c) Coefficient form : ( 1, 0, 0, 0, 1 ) Þ n + 1 = 5 \ n = 4 \ Index form : x4 + 0x3-0x2+0x+1 i.e. x4 + 1 Synthetic division : The following solved examples will illustrate this method. Example Divide the polynomial 2x3 - 20x + 5 by x - 3 Solution: i) We write the dividend in the coefficient form. ii) Since ( x - 3 ) is divisor, put 3 which is opposite of -3, at place of divisor and proceed as below:
Dividend = Divisor ´
Quotient + Remainder |
3.1 -
Introduction Follow @Pinkmonkey_com  |