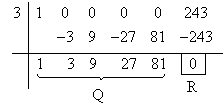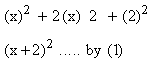Example Divide x5 + 243 by x + 3 Solution: Write the dividend in the coefficient form, and write -3 to the left of the 1st coefficient
\ x5 + 243 = ( x + 3 ) ( x4 - 3x3 + 9x2 - 27x + 81 ) + 0 FACTORING : Factor : When a number or an expression is the product of two or more numbers or expressions, each of the latter is called a factor of the former. Thus 4 and 7 are factors of 28 and ( x + y ) and ( x - y ) are factors of x2 - y2. Factoring or factorization is the process of changing any algebraic or numerical expression from a sum of terms into a product of factors. A number or expression is said to be prime if no factors can be obtained of that. 1. Expressions in which each term has a common factor. We have seen that x ( a + b + c ) = x a + x b + x c. We write this as x a + x b + x c = x ( a + b + c ) . ® ( 1 ) (1) shows that x and ( a + b + c ) are factors x a + x b + x c . Here we notice that every term on L. H. S. of (1) contains x as a factor. The other factor ( a + b + c ) can be obtained by dividing the given expression x a + x b + x c by the common factor x . Example Factorise 5x3 + 7x Solution: 5x3 + 7x = x (5x2 + 7 ) Example Find the factor of ap - aq + a r Solution: ap - aq + a r = a ( p - q + r ) Example Factorise 2m3 + 8m2 + 10m Solution: 2m3 + 8m2 + 10m = 2m ( m2 + 4m + 10 ) Example Find the factors of 2a3b - 8a2b2 Solution: 2a3b - 8a2 b2 = 2a2 b ( a - 2b ) Example Factorise c ( a + b ) + d ( a + b ) + e ( a + b ) Solution: c ( a + b ) + d ( a + b ) + e ( a + b ) = ( a + b ) ( c + d + e )
2. Factors by arranging terms in suitable groups. Example Factorise ac + bc + bd + ad + ae + be Solution: Here we cannot find a common factor. We can form suitable groups, thus expression = c ( a + b ) + d ( a + b ) + e ( a + b ) = ( a + b ) ( c + d + e ) or expression = a ( c + d + e ) + b ( c + d + e ) = ( c + d + e ) ( a + b ) = ( a + b ) ( c + d + e ) Example Resolve into factors x3 + 2x2y - 2xy2 - 4y3 Solution: x3 + 2x2y - 2xy2
- 4y3 = = x2( x + 2y ) - 2y2 ( x + 2y ) = ( x + 2y ) ( x2 - 2y2 ) Example ax - ay - bx + by + cx - cy Solution: expression = = a ( x - y ) - b ( x - y ) + c ( x - y ) = ( x - y ) ( a + b + c ) Perfect squares i) ( a + b )2 = a2 + 2 ab + b2 ii) ( a - b )2 = a2 - 2 ab + b2 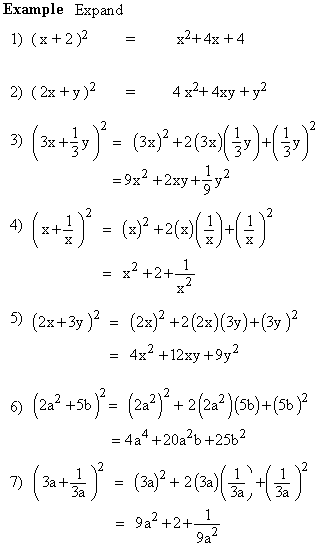
a2 + 2 ab + b2 = ( a + b )2 ..... (1) a2 - 2 ab + b2 = ( a - b )2 ......(2) Example Factorize x2 + 4x + 4 Solution: x2
+ 4x + 4= |
3.1 -
Introduction Follow @Pinkmonkey_com  |