Divisibility : We now take up the interesting ( and intriguing ) question as to now one can determine before - hand whether a certain number (however long it may be) is divisible by a certain divisor and especially as to the VEDIC process which can help us herein.

For this, we need certain special numbers know as "Ekadhikas".

(1) For 9, 19, 29, 39 etc. (all ending in 9), the Ekadhikas are 1, 2, 3, 4 etc.

(2) For 3, 13, 23, 33 etc. (ending in 3 ), multiply them by 3 and you get 1, 4, 7, 10 etc as the Ekadhikas.

(3) For 7, 17, 27, 37 etc. (ending in 7 ), multiply them by 7; and you get 5,12, 19, 26 etc. as Ekadhikas .

(4) For 1, 11, 21, 31 etc (all ending in 1) ; multiply them by 9 ; and you get 1, 10, 19, 28 etc. as Ekadhikas .

Osculation - Ekadhikas is our first osculator. Now suppose we do not know how to determine whether 21 is divisible by 7;

We multiply last digit 1 by Ekadhika ( or positive osculator i.e. 5 ) i.e. 1 ´ 5 = 5. Add this to previous digit i.e. 2 \ 2 + 5 = 7 which is divisible by 7 and yes, 21 is divisible by 7.

Consider 112, 2 ´ 5 + 1 Þ 11 ´ 5 + 1 = 56 yes 112 is divisible by 7 or 2 ´ 5 + 11 = 21 \ 112 is divisible by 7 .

Consider 322, 2 ´ 5 Þ 10 + 32 = 42 is divisible by 7 \ 322 is divisible 7

Consider 1393, 3 ´ 5 + 9 Þ 24 ´ 5 + 3 Þ 123 ´ 5 + 1 Þ 616, yes it is divisible by 7 \ 1393 is divisible by 7.

In this way one can get divisibility tests for almost all divisors. Thanks to 'VEDIC MATHEMATICS '. Still we suggest students to go for simple rules for divisibility as -

(1) A number is divisible by 2, if it ends in 0, 2, 4, 6 or 8.

For example 34, 62, 56, 88 are divisible by 2

(2) A number is divisible by ' 3 ', if the sum of its digits is divisible by 3.

For example, 354 is divisible by 3. Since the sum of digits of 354 is (3 + 5 + 4 = 12) which is divisible by 3.

(3) A number is divisible by 4, if the number obtained by the last two digits is divisible by 4. For example, 1556, the number obtained by last two digits is 56 which is divisible by 4. Therefore 1556 is also divisible by 4.

(4) A number is divisible by 5, if it ends in 0 or 5. For example, 210 and 315 are divisible by 5.

(5) A number is divisible by 6, if it is divisible by both 2 and 3 (i.e. use divisibility tests for both 2 and 3 )

For example, the number 216. It ends in 6 which is divisible by 2. Also the sum of digits of 216 is 2 + 1 + 6 = 9, which is divisible by 3. Therefore 216 is divisible by 6.

(6) For divisibility of 7, there is no simple test. (see osculation)

(7) A number is divisible by 8, if the number formed by its last three digits is divisible by 8.

For example, 2464 is divisible by 8, since ' 464 ' is divisible by 8.

(8) A number is divisible by 9, if the sum of its digits is divisible by 9.

For example, 3726 is divisible by 9, since 3 + 7 + 2 + 6 = 18 is divisible by 9.

In one problem, if multiplication, division, powers, addition, parentheses, etc. are all present, the order in which these operations are to be performed is as follows :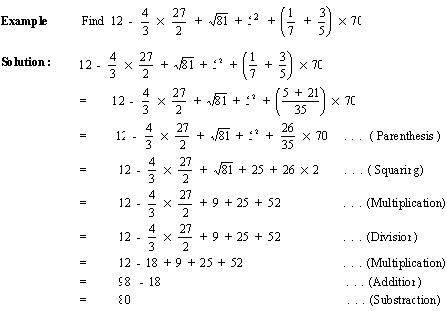

[next page]

Index

Introduction
1.1 Pre-requisties
1.2 Common Mathematical Symbols
1.3 Some Properties of Basic Mathematical Operations
1.4 Real Numbers

Chapter 2