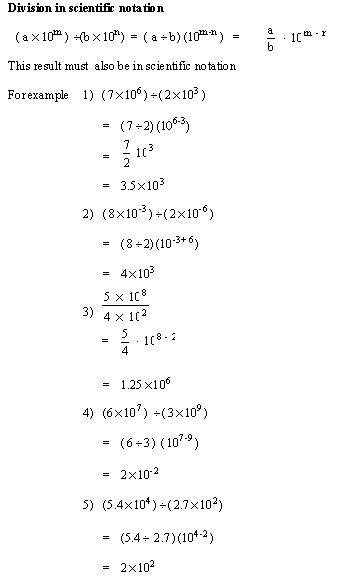|
Significant Figures : The specified number of digits which are accepted to denote the approximate value of a number, expressed as an integer and/or a decimal number. For example, a distance of 583275 km. can be taken as 583200 which is correct to four significant digits, the last two zeros are not significant as they denote the order of magnitude only. For example, 0.000745 has only 3 significant digits as the zeros in the beginning are used to denote the place value of the digits. Thus "Zeros at the end of a whole number or decimal may or may not be significant according to the degree of accuracy required but zero on the left is never the first significant figure." Example How many significant figures do the following numbers have? (1) 27.52 (2) 0.0001333 (3) 1.5637 ´ 105 (4) 0.003700 (5) 3.600 ´ 105 (6) 2,333,127
2) 0.000133 has 4 significant figures. 3) 1.5637 ´ 105 has 5 significant figures. 4) 0.003700 has 4 significant figures. 5) 3.600 ´ 105 has 4 significant figures. 6) 2,333,127 has 7 significant figures. Example A satellite moves 4.73 ´ 108 meters ( to three significant figures) in 10 hours. How many feet is this? 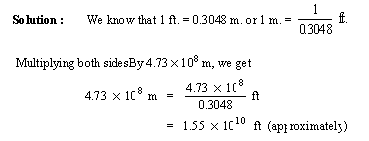
Since the original data is accurate to three significant figures, the answer is rounded off to three significant figures. Example Assume the earth is a sphere with the radius of 4000 miles. How many square inches of the surface area does the earth have? Solution : Surface area of the earth (sphere) = 4p r2 Now 1 mile = 5280 ´ 12 inches \ Surface area of the earth = 4p (5280 ´ 12 ´ 4000 )2 = 8.0726 ´ 1017 (inch)2
********** |
Introduction
Follow @Pinkmonkey_com 
|