Example 8 Find the area enclosed by the curve 4 y = x² and                    the straight line 3x - 2y - 4 = 0

Solution : Solving 4 y = x² and 3x - 2y - 4 = 0 we get

x² = 6x - 8 \ x² - 6x + 8 = 0 \ ( x - 2 ) ( x - 4 ) = 0

\ x = 2, x = 4 \ The points of intersection of the two are (2, 1) and (4,4). Therefore the required area enclosed between the straight line and the parabola is given by

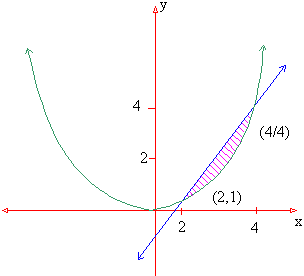
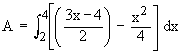
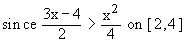
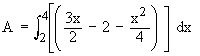
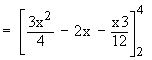
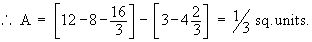
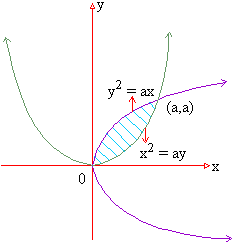
Example 9 Find the area enclosed between the two parabolas y² = ax and x² = ay.

Solution :   Solving   y²   =    ax   and    x²   =    a²y²  

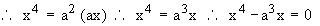
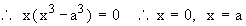
Therefore point of intersection of two parabolas are ( . 0, 0 ) and ( a, a ) and ( y² = ax ) > ( x² = ay ). Therefore the required enclosed between the two parabolas is

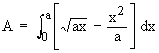
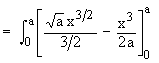
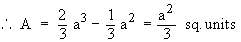
[next page]

Index

8.1 Introduction
8.2 Area
8.3 Volumes
8.4 Mean Value
8.5 Arc Length(Rectification)

Chapter 1