Example 5 Find the area of the region bounded by y = x3 + x2 - 12x and the x-axis.
Solution : Consider y = 0 to determine the points of intersection of the graph of y = x3 + x2 - 12x and the x-axis.
\
x3 + x2 - 12x = 0
\
x ( x2 + x - 12) = 0
\
x ( x + 4) (x-3) = 0
\
x = 0, x = -4, x = 2
\
Points of intersection are (-4, 0), (0, 0) and (2, 0) since f (x)3 0 on [ -4, 0 ] and f (x) £
0 on [ 0, 2 ], the area is given by
A = 
= 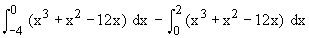
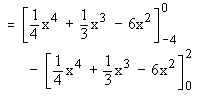
= 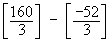
= 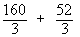
= 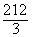
= 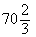
[next page]
|
Index
8.1 Introduction
8.2 Area
8.3 Volumes
8.4 Mean Value
8.5 Arc Length(Rectification)
Chapter 1
|