|
Example For the z-score, find the
probability that z lies between (i) 0 and 1.98 (ii) -0.68 and 0
(iii) 1.35 to 2.18 ( iv) -2.18 to - 1.35 (v) To the left of -0.6
(vi) To the right of z = -1.28 (vii) -2.18 to 1.35
Solution : Here
we are given z-scores, we have only to
refer to the table and find the areas
corresponding to these numbers and add or
subtract accordingly as the numbers are negative
or positive.
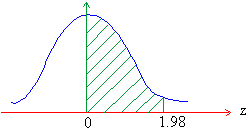
i) From the table z = 1.98 gives z = 1.98 is 0.4762
Thus P ( 0 £
z £
1.98 ) = 0.4762 i.e. 47% of area.
Note : For z = 1.18 looking into the table of z-score, first find 4.9 in the first column and move to your right along the same horizontal row till you get column with head 0.08. The intersection of the two is 0.4762 (refer to Table 1)
See this ®
First column 0.01 0.02 .............0.08 0.09
z)
1.9 0.4713 0.4719
............  0.4767
0.4767
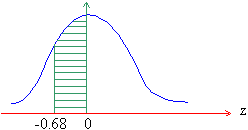
- Area from z = -0.68 to 0 is the same as from 0 to 0.68 by symmetry.
hence for z = 0.68 it is 0.2518.
\
P ( -0.68 £
z £
0 = 0.2518 i.e. 25% of area.
iii) Area from 0 to 1.35 is 0.4115 and from 0 to 2.18 is 0.4854. The required area is the difference between the two areas.

\
P ( 1.35 £
z £
2.18 = 0.4854
- 0.4115
= 0.739
i.e. 7% of area.
[next page]
|