|
Significance of Moment of Inertia
Consider Equations (1) , (4) , (6) as above viz,
These equations are analogous to corresponding equations for a particle in translational motion.
The similarity pointed out above between translational motion of a particle and rotational motion of a rigid body can be extended to any equation for the translational motion to the obtain corresponding rotational motion equations,
The table below lists these similarities.
Note : For a discrete system of particles the |
5.1 Rotational motion of a rigid body about a fixed axis Follow @Pinkmonkey_com  |

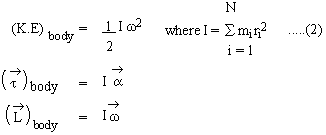
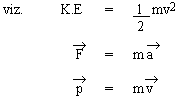
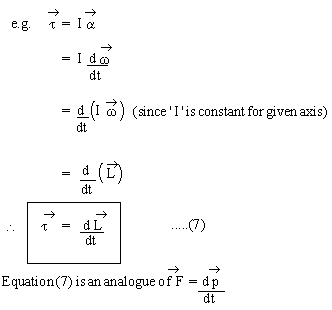

 where as for a continuous system of particles I =ò dm r2
where as for a continuous system of particles I =ò dm r2