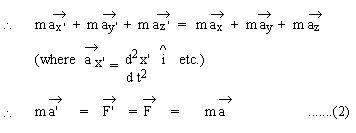35.2 Galilean Principle of Relativity and Invariance of Newton's Laws of motion
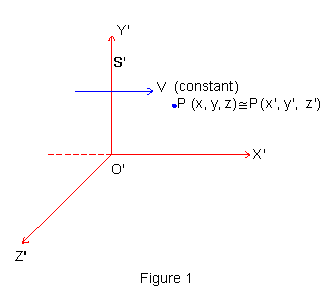
If O' and O are coincident at t = 0
Thus, the law of motion of Newton is invariant under transformation from one to another frame in a relative uniform translational motion with respect to each other. Therefore, S' is also an inertial frame if S is an inertial frame.
Note In writing down equations (1), we have tacitly assumed that length and time measurements are not affected by the State of motion of the rods and clocks. The same assumption has been made in writing down Equation (2) for mass i.e., mass of an object is independent of the frame of references in which it is measured. The invariance of Newton's laws of motion under Galilean Transformation between two inertial frames in relative uniform translational motion with respect to each other implies the Galilean Principle of Relativity: "It is impossible to distinguish between the two inertial frames by performing any mechanical experiment completely within any given frame of reference." |
35.1 Frames
of References Follow @Pinkmonkey_com  |