|
The transverse wave in figure (6a-1) produced by oscillating the free end of rope in the plane of diagram - perpendicular to its length is not obstructed by the slit, but in figure (6a - 2) it is obstructed by the slit and therefore, the wave does not pass through the slit. The part of rope beyond the slit remains at rest along horizontal.
The longitudinal wave in figure 6(b), that is produced by oscillating the rope along the horizontal direction, is not obstructed by a slit kept in any position and therefore the wave always passes through the slit.
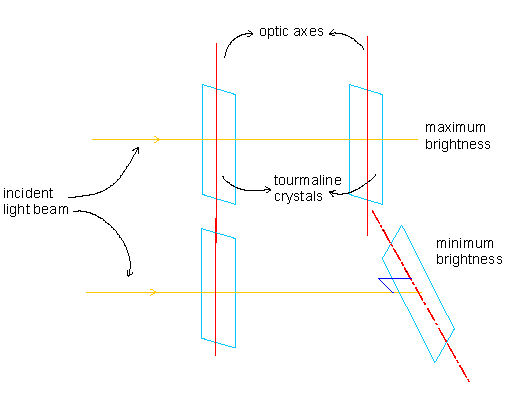
Consider that a beam of light, say from sodium vapor lamp, is incident on a tourmaline crystal. Let another identical tourmaline crystal be kept behind the first. Observe the brightness of light as it comes out of the second crystal, which is being rotated about the path of light, as the axes of the rotation. It will be observed that the brightness of light is maximum when the reference axes (called optic axes) of both the crystals are parallel to each other and the brightness is minimum (almost dark) when the optic axes are perpendicular to each other. This observations implies that light is a transverse wave and is polarized by the first crystal such vibrations are restricted along the optic axes. Therefore, when the second crystal has its optic axes parallel to the first the vibrations pass through it, but when the second crystal's optic axes is perpendicular to that of the first the vibrations cannot pass through it. (see figure 7a & 7b.)
Figure 7(b)
********** |
18.1 Interference
of light Follow @Pinkmonkey_com  |