|
Theorem 1 : If the co-ordinates of two points are (x1,
y1) and (x2, y2), then the distance
d between them is given by the formula :
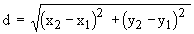
Example 1
Using the distance formula determine the distance between the points with co-ordinates ( 4, -2 ) and (6, 3 ).
Solution :
Let (4, -2) be (x1, y1) and
(6, 3) be (x2, y2). Then according to the distance formula,

Example 2
A triangle has vertices A (2,2), B (5,2) and C (5,6). Show that the triangle is a right angled triangle.
Solution :
By the distance formula

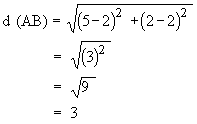

\
d(AC) = 5, d (AB) = 3, and d (BC) = 4
According to Pythagorean if the sum of the square of two sides are equal to the square of the third side then the triangle is a right angled triangle.
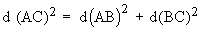
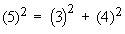
Therefore, the triangle is right angled triangle.
[next page]
|