2.5 Congruence of triangles
Two triangles are said to be congruent, if all the corresponding parts are equal. The symbol used for denoting congruence is @ and
D PQR @ D STU implies that
 and also and also 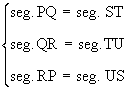
i.e. corresponding angles and corresponding sides are equal.
In order to prove that two triangles are congruent, it is not always necessary to show that all the six corresponding parts are equal. If certain basic requirements are met the triangles are said to be congruent. These basic criterias are embodied in the five postulates given below. These postulates are axiomatic and are useful in proving the congruence of triangles.
S S S Postulate
If all the sides of one triangle are congruent to the corresponding sides of another triangle then the triangles are congruent (figure 2.15 ).
Figure 2.15
seg. AB = seg. PQ , seg. BC = seg. QR and
seg. CA = seg. RP
\ D ABC @ D PQR by S S S.
S A S Postulate
If the two sides and the angle included in one triangle are congruent to the corresponding two sides and the angle included in another triangle then the two triangles are congruent (figure 2.16).
Click here to enlarge
Figure 2.16
seg. AB = seg. PQ , seg. BC = seg. QR and
m Ð ABC = m Ð PQR
\ D ABC @ D PQR by S A S postulate.
A S A Postulate
If two angles of one triangle and the side they include are congruent to the corresponding angles and side of another triangle the two triangles are congruent (figure 2.17 ).
Figure 2.17
m Ð B + m Ð R m Ð L = m Ð P and seg. BC = seg. RP
\D ABC @ D QRP by A S A postulate.
A A S Postulate
If two angles of a triangle and a side not included by them are congruent to the corresponding angles and side of another triangle the two triangles are congruent (figure 2.18)
Figure 2.18
m Ð A = m Ð P m Ð B = m Ð Q and AC = PR
\ D ABC @ D PQR by A A S.
H S Postulate
This postulate is applicable only to right triangles. If the hypotenuse and any one side of a right triangle are congruent to the hypotenuse and the corresponding side of another right triangle then the two triangles are congruent (figure 2.19).
Figure 2.19
Then hypotenuse AC = hypotenuse PR
Side AB = Side PQ
\ D ABC @ D PQR by HS postulate.
|