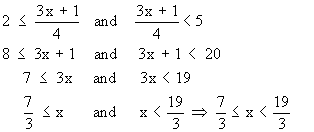| Example Solve and graph Solution : First we rewrite this statement into two inequalities and then solve
Thus a solution must be greater and equal to So the solution set
Example Solve 2 x - 1 £ 4 x - 3 < 6 x + 3. Graph also Solution : 2 x - 1 £ 4 x - 3 and 4 x - 3 < 6 x + 3 2 £ 2 x and - 6 < 2 x 1 £ x and -3 < x The two solutions at the same time are { x | x ³ 1} { x | x > -3} and thegraph is 1 £ x :
-3 < x :
Thus 1 £ x and -3 < x Þ {x | x ³ 1 } Ç {x | x > -3 }
= {x | x ³ 1 } = [ 1, ¥ ]
|
7.1 Definition |
and less than 
at the same time .
