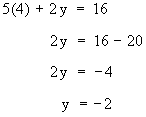| Example Solve 3 x - 5 y = 16; x - 3 y = 8 Solution: 3 x - 5 y = 16 . . . (1) x - 3 y = 8 . . . (2) To make the coefficients of x equal, by multiplying the equation (2) by 3 we get
3 x - 9 y = 24 . . . (3) For eliminating x, subtract equation (3) from (1) 3 x - 5 y = 16 . . . (1) 3 x - 9 y = 24 . . . (3) (-) (+) (-) 4 y = - 8 y = - 2 Inserting y = -2 in (1), (2) or (3). But it is convenient to insert this value in equation (2)
\ x - 3 (-2) = 8
\ x + 6 = 8 \x = 8 - 6
\x = 2 Therefore, x = 2, y = -2 is the required option. Example Solve 2 x - 3 y = 14; 5 x + 2 y = 16 Solution: 2 x - 3 y = 14 . . . (1) 5 x + 2 y = 16 . . . (2) If we multiply (1) by 2 and (2) by 3 the coefficients of y will be numerically equal By multiplying (1) by 2; 4 x - 6 y = 28 . . . (3)
By multiplying (2) by 3; 15 x + 6 y = 48 . . . (4) Adding (3) and (4), y will be eliminated as
19 x = 76 \ x = 4 Inserting x = 4 in (2) we get
Therefore, x = 4, y = -2 is the solution
|
7.1 Definition |